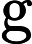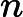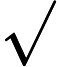BDA3 Chapter 3 Exercise 5
Here’s my solution to exercise 5, chapter 3, of Gelman’s Bayesian Data Analysis (BDA), 3rd edition. There are solutions to some of the exercises on the book’s webpage.
Suppose we weigh an object 5 times with measurements
measurements <- c(10, 10, 12, 11, 9)all rounded to the nearest kilogram. Assuming the unrounded measurements are normally distributed, we wish to estimate the weight of the object. We will use the uniform non-informative prior .
First, let’s assume the measurments are not rounded. Then the marginal posterior mean is .
Now, let’s find the posterior assuming rounded measurements. The probability of getting the rounded measurements is
where is the CDF of the distribution. This implies that the posterior is
Calculating this marginal posterior mean is pretty difficult, so we’ll use Stan to draw samples. My first attempt at writing the model was a direct translation of the maths above. However, it doesn’t allow us to infer the unrounded values, as required in part d. The model can be expressed differently by considering the unrounded values as uniformly distributed around the rounded values, i.e. .
model <- rstan::stan_model('src/ex_03_05_d.stan')modelS4 class stanmodel 'ex_03_05_d' coded as follows:
data {
int<lower = 1> n;
vector[n] y; // rounded measurements
}
parameters {
real mu; // 'true' weight of the object
real<lower = 0> sigma; // measurement error
vector<lower = -0.5, upper = 0.5>[n] err; // rounding error
}
transformed parameters {
// unrounded values are the rounded values plus some rounding error
vector[n] z = y + err; // unrounded measurements
}
model {
target += -2 * log(sigma); // prior
z ~ normal(mu, sigma);
// other parameters are uniform
} Note that Stan assumes parameters are uniform on their range unless specified otherwise.
Let’s also load a model that assumes the measurements are unrounded.
model_unrounded <- rstan::stan_model('src/ex_03_05_unrounded.stan')model_unroundedS4 class stanmodel 'ex_03_05_unrounded' coded as follows:
data {
int<lower = 1> n;
vector[n] y;
}
parameters {
real mu;
real<lower = 0> sigma;
}
model {
target += -2 * log(sigma);
y ~ normal(mu, sigma);
} Now we can fit the models to the data.
data = list(
n = length(measurements),
y = measurements
)
fit <- model %>%
rstan::sampling(
data = data,
warmup = 1000,
iter = 5000
)
fit_unrounded <- model_unrounded %>%
rstan::sampling(
data = data,
warmup = 1000,
iter = 5000
) We’ll also need some draws from the posteriors to make our comparisons.
draws <- fit %>%
tidybayes::spread_draws(mu, sigma, z[index]) %>%
# spread out z's so that
# there is one row per draw
ungroup() %>%
mutate(
index = paste0('z', as.character(index)),
model = 'rounded'
) %>%
spread(index, z)
draws_unrounded <- fit_unrounded %>%
tidybayes::spread_draws(mu, sigma) %>%
mutate(model = 'unrounded')
draws_all <- draws %>%
bind_rows(draws_unrounded)| mu | sigma | model | z1 | z2 | z3 | z4 | z5 |
|---|---|---|---|---|---|---|---|
| 9.89706 | 1.878745 | rounded | 9.577059 | 9.843934 | 11.53135 | 10.84123 | 9.018176 |
| 10.14826 | 1.415935 | rounded | 9.624707 | 9.816654 | 11.58052 | 10.63842 | 8.809419 |
| 11.54313 | 3.284362 | rounded | 9.696221 | 10.137208 | 12.04615 | 10.65639 | 9.369857 |
| 11.55348 | 1.379274 | unrounded | NA | NA | NA | NA | NA |
| 11.64592 | 1.454829 | unrounded | NA | NA | NA | NA | NA |
| 11.91674 | 2.999751 | unrounded | NA | NA | NA | NA | NA |
The contour plots look very similar but with shifted upward when we treat the observations as unrounded measurements. This is contrary to my intuition about what should happen: by introducing uncertainty into our measurments, I would have thought we’d see more uncertainty in our parameter estimates.
The density for look much the same in both models. This is expected because the rounded measurement is the mean of all possible unrounded measurements.
The marginal posterior for again shows a decrease when taking rounding error into account. I’m not sure why that would happen.
| model | 5% | 50% | 95% |
|---|---|---|---|
| rounded | 0.6050823 | 1.022847 | 2.034147 |
| unrounded | 0.6780966 | 1.088672 | 2.118638 |
Finally, let’s calculate the posterior for (assuming we observe rounded measurements).
sims <- draws %>%
mutate(theta = (z1 - z2)^2) There is a lot of mass near 0 because the observed rounded measurments are the same for and . The probability density is also entirely less than 1 because the rounding is off by at most 0.5 in any direction.